01产线产量计算
在说明量价关系之前,让我们来看看年产量与哪些方面有关。每一年能够做出的产品数量和生产时间和单位时间内的生产效率有关,而我们要做的就是需要将其再进行细化,找出内含的关系。

每小时生产零件数Nt=3600/[t/n*(1+U)+60T/C)]
t/n*(1+U) 首先是将循环时间÷循环生产零件数,得到每一个零件的生产时间;再算上意外停机率的影响,得到零件的理论生产时间。
60T/C 此处考虑了换模(换型)的时间和在此期间需要准备的库存数量,得到单个零件的需要承担的换模时间。
将单个零件的理论生产时间加上需要承担的换模时间,就可以得到单个零件的完整循环时间,那么小时生产零件数Nt也就浮出水面了。
每小时实际生产零件数Na=3600*(1-M)/[t/n*(1+U)+60T/C)]
1-M 也就是100%-废品率,得到生产过程中的良品率。将良品率乘以刚才得到的每小时生产零件数就可以得到每小时实际生产零件数Na了。Nt与Na的区别在于是否考虑了良品率,可以说Nt是考虑能够做几个,而Na则是将质量的因素考虑其中,考虑的是能够做几个合格品。
每年实际生产零件数N=3600*(1-M)/[t/n*(1+U)+60T/C)]*H*R=Na*H*R
H是车间一年可投产时间,乘上R设备开动率,即可得到车间年实际投产时间,再乘以上面的Na,即可得到一年的实际生产零件数。
02汽车量价关系的发展
分享人在研究汽车量价关系时,参考了如下资料:
2007年:喻湘存和熊曙初所著的《系统工程教程》中提出“产量-成本-盈利”分析法。
2010年:周康渠等所写的《某汽车企业零部件采购量价模型分析》中根据“产量-成本-盈利”分析法,建立的采购量价模型。
“产量-成本-盈利”分析法
需要注意的是该方法基于以下的六大假设,有一定的限制条件,与实际的市场情况并不是完全相符的。
销售收入与销售量呈完全线性关系:说明价格没有波动,和实际市场情况不同,并不会随着时间的推移而有降价的情况。
变动成本与产量呈完全线性关系:例如材料费用等是固定不变的,不会受到市场的采购价格的波动或者是不同批次中由生产差异导致的材料费用波动。
固定成本保持不变:如果不进行人员增减或者产线的投入,实际中可以做到固定成本不变。
产销平衡:也就是没有库存的说法,生产方每生产出一个产品,就会把它卖掉。
品种结构不变:该模型只针对单一品种的产品,如果有多种产品,会各自分开单独计算。
会计数据可靠:数据符合会计上的相关定义,是真实有效的。
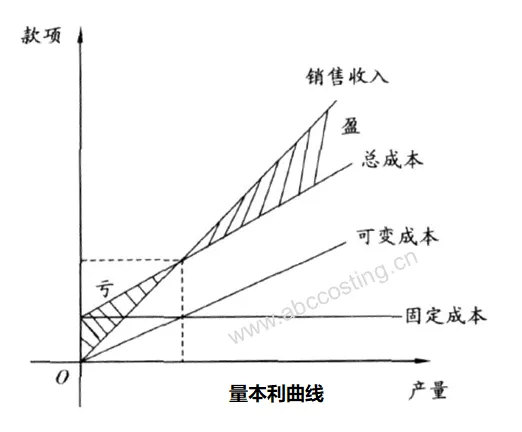
基于上述的价格,我们得到了本量利的两个关系式:
基本关系P=(p-b)*x-a

P代表利润,p是单价,b代表变动成本,x为销量,a为固定成本
贡献边际关系P=p*x-b*x-a
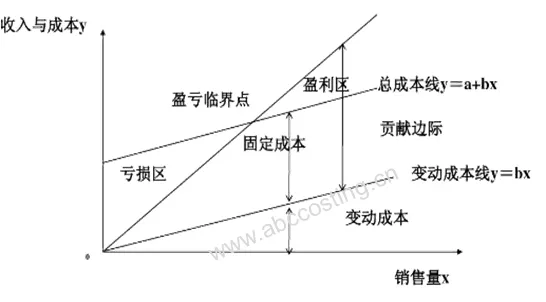
本量利的贡献边际关系P=p*x-b*x-a,C=b*x+a为总变动成本
相信很多小伙伴对这两个关系式还是比较熟悉的,公式简单参数少,道理简单。虽然是一个比较理想化的模型,但当我们将这个模型中的数字进行进一步的拆解和细化,将因子尽可能的打散,找到更多的关系式,再基于实际的数据进行分析,可以得到一定条件下的更符合实际应用场景的模型。
采购量价模型
基于上面的量本利模型,利润为P, 单位产品售价为K, 产量为Q, 产品固定成本为F, 可变成本为V。
则总成本=固定成本+变动成本=固定成本+单位产品平均可变成本*产量,即 C=F+V=F+v*Q。其中v=V/Q,称为单位产品平均可变成本。
根据“产量-成本-盈利”分析法可得利润=售价*产量-总成本,即P=K*Q-C, 那么产品售价=(固定成本+利润)÷产量+单位产品平均可变成本,即 K=(F+P)/Q+v
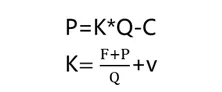
让我们将关系式进一步进行分解,可以得到
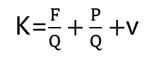
假设P/Q不变,也就是单个零件零件利润与产量无关, 且v不受产量或价格变动而改变或改变很小时, 可将P/Q+v视为常数, 令P/Q+v=a, a为常数,则:
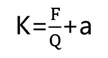
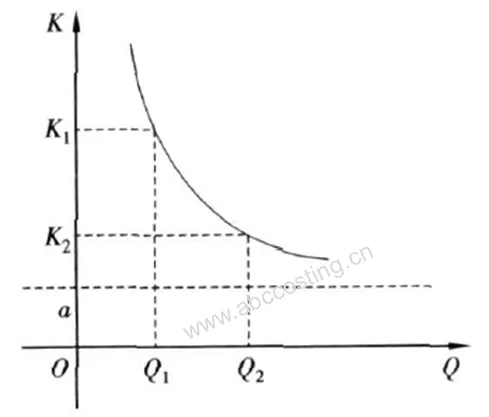
得到上述关系式之后,接下来要做的工作就是固定成本F细分再细分,尽可能的找出影响成本的因子。
a. 确定成本的构成部分,也就是将料工费进行再拆解。根据经验我们可以拆为如下的一些类目,此处的制造费是一个狭义的概念,可以理解为是在产品制造过程中发生的费用,但不能归集到其他类目的费用。

b. 假设在各成本项中,固定成本和可变成本可以按照一定的比例进行分配, 比例之和为100%, 那么单个零部件的固定成本是各成本项中固定成本之和, 即:

fi为各成本项;li为各成本项所对应的固定系数;n为成本项数;F为单个零部件固定成本
c. 当采购量为Q0时,零部件的总固定成本为

d. 当采购量Q_1为时, 零部件的总固定成本为

经过再推导采购量改变后每项成本
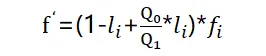
公式有点绕,下面来看一个例子。需要注意的是其中所使用的固定和变动成本的比例是基于某公司的历史数据而得到的经验值,这个系数并不是一成不变的,实际工作中需要根据自身情况进行总结和调整。
下图为某一企业的成本变动系数表:
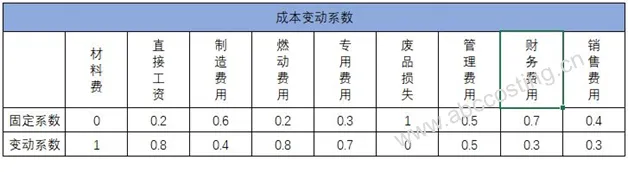
根据该表,采购量为10万件时,各项成本如下:
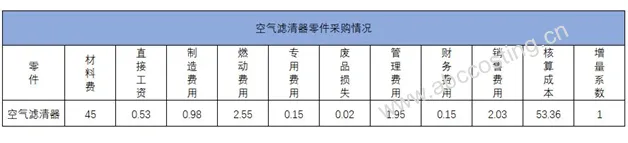
采购量为20万件时,增量系数为2,此时各项成本计算为
材料费f_1=(1-0+1/2*0)*45=45元
直接工资f_2=(1-0.2+1/2*0.2)*0.53=0.48元
制造费用f_3=(1-0.6+1/2*0.6)*0.98=0.69元
燃动费用f_4=(1-0.2+1/2*0.2)*2.55=2.30元
专用费用f_5=(1-0.3+1/2*0.3)*0.15=0.13元
...
销售费用f_9=(1-0.4+1/2*0.4)*2.03=1.62元
核算成本f=f_1+f_2+f_3+……+f_9=51.78元
即当采购量为20万件时,成本为51.78元。
采购量价模型的局限性
通过上面的例子,大家应该也发现了这个模型的局限性。
只能适应于采购量少于一条生产线的年产量
条件比较理想化
不同行业成本变动系数不同,成本变动系数较难获取
计算比较复杂
如前文所提,这个采购量价模型是一个非常理想化的模型,意在想要通过大数据分析,将每一个成本因子都能够与采购单价有着一定的线性关系,这个模型可以帮助大家对成本进行更深层次的思考。
03我认为的量价关系
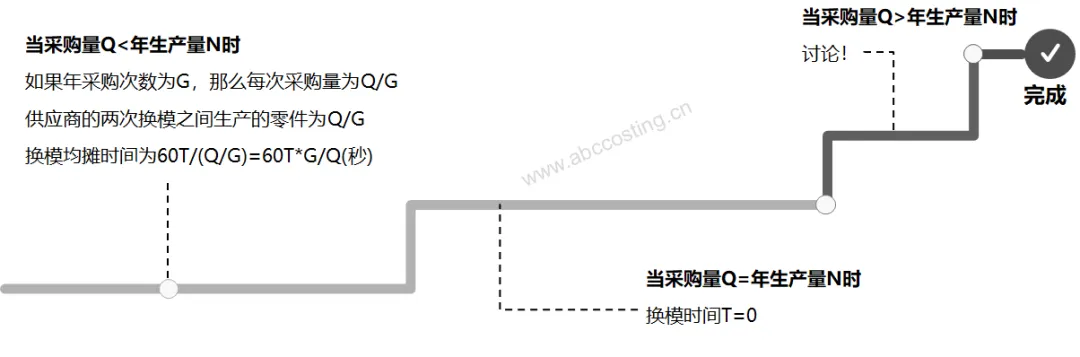
基于上面的模型,结合实际工作所遇到的各种场景,我们可以将采购量Q与年生产量N的关系分为三段:
采购量Q<年生产量N
在这个阶段,产线产能仍有富裕,因此在满足采购订单的情况下,会有换模(换型)动作,从而去生产其他产品,使产线的利用率提高。此时就需要将考虑换模均摊时间。
采购量Q=年生产量N
采购量Q和产线年生产量N一致,即产线不用进行换模(换型)即可达到最大的生产利用率。
采购量Q>年生产量N
当采购量Q超过年生产量N的时候, 这种情况下就需要单独讨论了。此时可能会需要一些额外的产线投资,那么固定成本就会上升,之前所使用的系数也会需要进行调整。
话不多说,再来个例子。
问:假设冲压通用设备费用1000万元,工序人数为2人,每人每年支出为8万元,水电热支出为4.8万元。
循环时间为10秒,一模一件,换模时间为30分钟,意外停机率为1%,车间年可投入时间为4,518小时,设备开动率为80%,报废率为3%。
根据之前的公式,可以得出产线每年最大实际生产零件数
N=3600*(1-M)/[t/n*(1+U)+60T/C)]*H*R
=3600*(1-3%)/[10/1*(1+1%)+0)*4518*80%
=1,249,652件。(此时换模时间为0)
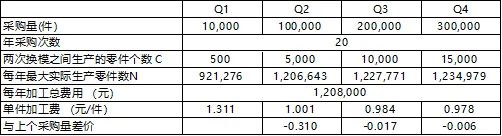
求:假设年采购次数均为20次,那么在采购量1万、10万、20万和30万的时候,产品单价件加工费用为多少?
答:加工费总额=1000万/10+8万*2+4.8万=120.8 万元/年
首先我们需要将采购量Q除以采购次数,得出每一次的采购数量,这数量就是两次换模时间之间生产的零件数C。接着就可以套用公式进行计算,结果如下:
04最佳库存量
通过上面的例子我们可以发现,在其他条件固定的情况下,每次的采购量会影响着加工费用,那么我们该如何确定每一次的最佳采购量呢?假设有如下影响因子:
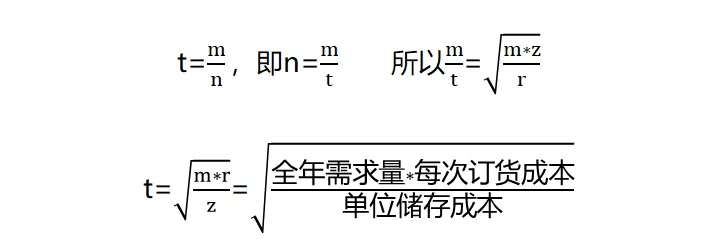
全年需求量=m; 每次订货成本=r; 单位储存成本=z; 采购次数=n; 最优采购量=t
我们的需求的是m/n∗z+n*r的结果最小,可推出当m/n∗z=n*r时,结果最小,所以当n为如下值时满足结果。

(想知道这里的结果为啥突然开了个根号,往下看~有分享人手稿解释哦)
最优采购量t=全球需求量÷采购次数,那么我们将上面得到的最佳n值代入
采购量、订货成本和储存成本是相互制约的,现在我们追求的是最佳采购量,根据工具可知即是需要当储存成本和订货成本的关系最优时,才对得到最佳采购量。
从小编角度来说,前面的量价关系及其衍生关系还是容易理解的,但跳到最佳采购量这一段,概念上可以理解,公式上理解不易,附上分享人特意画的手稿给大家琢磨一下。不得不说虽然小编的高数已经忘光光,但看了之后茅塞顿开,给花容点个赞。
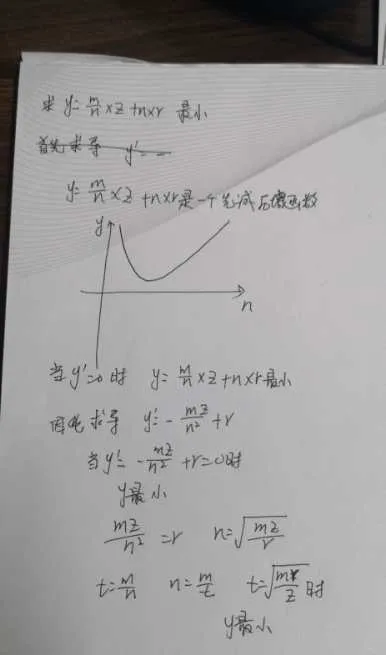
05答疑解惑
1. 最佳采购量中提到的订货成本具体包括哪些费用呢?
包括但不限于产品的运输成本;与采购活动相关的一些人工成本,例如由于需要采购去出差所发生的差旅费等。具体还是要根据公司实际情况来进行判断。
2. 公式中的单次需求量是根据全年平均采购量得出的平均单次需求量,那在实际工作中,单次需求量并不是一个很平均的状态,会有单次的需求量比较高的时候,该怎么处理呢?
就像分享时提到过的,这是一个理想的模型,实际生产中采购量会根据需求波动,并不能一概而论。模型可以帮助大家找到成本与每个因子之间的联系,这个联系是客观存在但又不是一成不变的,不过模型可以帮助你估算出一个合理的需求量的范围,从而调整订单以达到降低采购成本的目的。
作者:ABC花容
来源公众号:ABC成本分析
原题:关于采购量价关系的讨论





评论区